
deep space computing AG is able to implement solutions to problem that can be solved with Linear Programming. We use the GLPK (GNU Linear Programming Kit) to implement our solutions. As soon as there will be Linear Solvers running on GPUs, deep space computing is committed to deliver them to customers through the Computational Cluster.
Center of the model is an objective function expressed over a feasible region. The objective function is linear and is expressed with the linear coefficient vector c .
The feasible region is a convex polyhedron with the same dimensionality of c , bounded by a set of linear inequality constraints representing limits in the model. Additional linear equalities define conservation laws and current stati of the system. All linear equalities and inequalities are expressed in the matrix A and vector b.
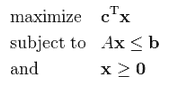
The linear programming algorithm Simplex, originally developed at IBM, finds a point in the polyhedron where this function has the largets value if such a point exists.
Before running the algorithm, it is necessary to convert the problem in augmented form. This form introduces non-negative slack variables to replace inequalities with equalities in the constraints. The problems can then be written in the following block matrix form:
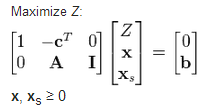
where xs are the newly introduced slack variables, and Z is the variable to be maximized.
Here a simple example of a hydro power plant optimization done by deep space with GLPK:









